


不确定度、准确度、精度这三个名词在计量研究报告、测试报告及仪器性能说明中经常出现,许多人对这些常见的计量测试名词含义不清,出现错用的现象,搞清这些专业术语,了解其本质含义及区别,对从事计量测试的技术人员来说具有重要的现实意义。
不确定度定义为与测量结果相关联的参数,表征合理地赋予被测量值的分散性。它可以是标准偏差,也可以是说明了置信水平的区间半宽度,经常用标准不确定度、合成不确定度、扩展不确定度来表示。
测量准确度定义为测量结果与被测量真值的一致程度。真值在实际测量中是较难得到的,故准确度只是一个定性的概念,所谓定性意味着可以用准确度的高低、准确度为0.25级、准确度为3级、准确度符号XX标准等说法定性地表示测量质量。
精度是用来表示测量结果中的随机误差大小的程度,反映的是在规定条件下各独立测量结果间的分散性。在测量误差理论中,精度或精确度常出现,我国长时间以来一直习惯用精度这一名词,如在仪器性能表示中经常出现这一名词,它有时指精密度,有时指准确度,比较混乱,在计量测试报告中尽量回避精度这一提法。
准确度或精度是与测量误差相关联的,表示的是测量结果与真值的偏离量,因此是一个确定的值,在数轴上表示为一个点。测量不确定度表示被测量之值的分散性,它是以分布区间的半宽度表示的,因此在数轴上是一个区间。
严格来说,准确度与精(密)度是有区别的,准确度是测量结果中系统误差与随机误差的综合表示,是一个定性的概念,而精度是表示测量结果中随机误差的大小。一个仪器的精度高,不能就说它的准确度一定高,精度高只说明其测量的随机误差小,但是准确度高必须使随机误差与系统误差都小。
测量结果的不确定度表示在重复性或复现性条件下被测量之值的分散性,其大小只与测量方法有关,即测量原理、测量仪器、测量环境条件、测量程序、测量人员、以及数据处理方法等有关,而准确度或精度是与测量误差有关,而误差仅与测量结果及真值有关,而与测量方法无关。
对模拟输出的仪表,主要给出其精度,其形式有两种,其一是%读数+%满量程,如某仪器测量直流电流的精度为0.01%+0.0015%;其二是精度等级,如±0.05%。给定精度,就可以得出单次测量的最大误差,以某仪器测量直流电流为例,如果所用的电流档为1A,某次仪表示值读数为0.5A,则该次测量的最大误差为
0.5A*0.01%+1A*0.0015%=0.065mA
对数字量输出的仪表,常以准确度的形式给出,此时的准确度(定量)与前面模拟输出仪表给出的精度含义相同,其基本形式为:%读数+X个字,如FLUKE715电压/毫安(V/mA)校准器给出的电压测量准确度为0.02%读数+2个字。
不确定度是以标准不确定度、合成不确定度、扩展不确定度表示的,总体来说,有两种表现形式,一种是绝对形式,另一种是相对形式。绝对形式表示的不确定度与被测量有相同的量纲,相对形式的不确定度无量纲。被测量x的标准不确定度u(x)和相对标准不确定度urel(x)之间的关系为

式中的x为被测量的真值,常用其约定真值或真值的最佳估值代替。
同样,扩展不确定度与合成标准不确定度也有绝对形式与相对形式。在计量报告中,测量结果一般以扩展不确定度的形式给出,其一般形式为
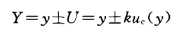
式中:y是被测量的最佳估值;U为扩展不确定度;uc(y)为合成标准不确定度;k为包含因子。该式的含义是:被测量的最佳估值是y,由y-U到y+U的区间,包含了能合理赋予y的分布的大部分。
准确度与随机误差与系统误差有关,而精度只与随机误差有关,无论是随机误差还是系统误差都与无数次的测量的平均值有关,它们都是理想化的概念,实际只能得到它们的估值,故可可操作性角差。精度的计算过程如下:
测量某值,在相同的情况下连续测量n次(n足够大),得到的测量值为x1、x2、x3……xn。
计算测量值的数学期望M(x):

计算测量值的方差δ²(x):
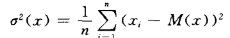
δ(x)是方差的额算数平方根,即标准偏差,其大小反映了精度的高低。
不确定度可以根据实验、资料、经验等信息进行评定,是可以定量操作的。标准不确定度的评定方法可分为A类与B类,而扩展不确定度及合成标准不确定度的计算都是建立在标准不确定度的基础上。
用对被测量重复观察并根据测量数据进行统计分析的方法来评定标准不确定度,称为标准不确定度的A类评定方法。常用以下几种方法:
1) 对被测量X,在同一条件下进行n次重复观察,观察值(x1、x2、x3……xn)。则
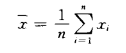
`X是被测量X的估计值,即测量结果。`X的试验标准偏差s(`X)即为测量结果的标准不确定度u(x)
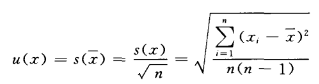
2) 对于一个测量过程,若采用核查标准和控制图的方法使测量过程处于统计控制状态,则统计控制下测量过程可用合并标准差Sp表征。若每次核查的自由度相同,则
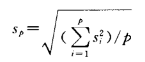
式中:Sp为合并标准偏差,是测量过程长期组内标准偏差的统计平均值;Si为每次核查的样本标准偏差;P是核查次数。
由该测量过程对被测量X进行n次观察,其测量结果的标准不确定度为
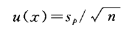
3) 当被测量X的估计值是由实验数据用最小二乘法拟合的一条直线或曲线上得到时,任意预期的估计值或表征曲线拟合参数的标准不确定度可以用已知的统计程序计算得到。
当被测量X的估计值不是由重复观察得到时,标准不确定度的评定就可用B类方法,B类评定主要是利用X的有关信息或资料来评定,包括以前测量的数据、一般的认识、生产厂的技术说明书、检定证书、测试报告、引用手册等。具体方法如下:

根据经验或资料等有关信息,分析判断被测量可能的区间(-a,a),并假设被测量值的概率分布,由要求的置信水平估计包含因子k,则B类评定的标准不确定度为
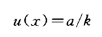
上一篇:变频器开关频率的影响