谐波

• 浏览次数：36681次
• 发布时间：2013/9/18 15:57:34
• 作者：hb­_yinhe

一谐波相关定义

　　谐波的英文为：harmonic，

　　《GB/T2900.1-2008 电工术语 基本术语》对谐波的定义是：

　　周期量的傅里叶级数式中阶次大于1的分量。

　　根据傅立叶等人提出的谐波分析方法——傅里叶变换，满足Dirichlet条件的、以T为周期的周期函数f(t)，在连续点处，可以展开为常数与一组具有共同周期的正弦函数和余弦函数之和，并可用下述三角函数的线性组合来表示：

　　上式称为f(t)的傅里叶级数，其中，ω=2π/T。

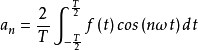
　　n为整数，n≥0。

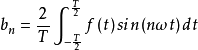
　　n为整数，n≥1。

　　在间断点处，下式成立：

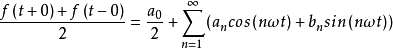
　　a₀/2为信号f(t)的直流分量。

　　令

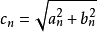
　　c₁为基波幅值，c_n为n次谐波的幅值。c₁有时也称一次谐波的幅值。a₀/2有时也称0次谐波的幅值。

　　谐波的频率等于基波的频率的整数倍，基波频率3倍的波称之为三次谐波，基波频率5倍的波称之为五次谐波，以此类推。不管几次谐波，他们都是正弦波。

　　采用傅里叶变换，方波可以分解为基波和3、5、7、11、13……次谐波的组合，n次谐波含量是基波的1/n。

　　下图形象的再现了通过基波、3、5、7次谐波合成近似方波的过程。

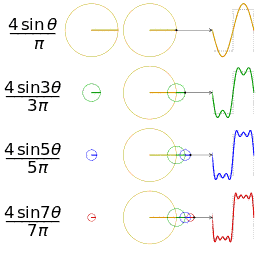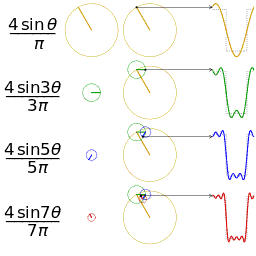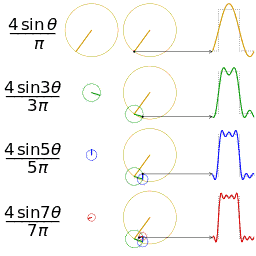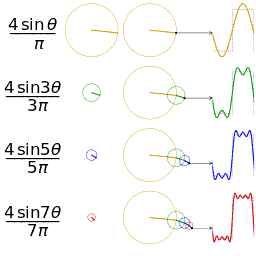
谐波构成方波的动画演示

二谐波产生原因

　　要理解谐波产生的原因，首先要理解什么才叫不含谐波？

　　在理想的干净供电系统中，电压是纯正的正弦波的。连接在电网上的线性负荷稳定运行时，流过的电流是正弦波。连接在电网上的非线性负荷中流过的电流是非正弦波。

01谐波电流产生原因

　　只要不是单一频率的正弦波，就包含谐波。

　　而单一频率的正弦波，频率和幅值都是恒定的。换言之，只要频率和幅值之一发生变化，就说明产生了谐波。

　　最简单线性负荷的例子是白炽灯，因为白炽灯相当于一个电阻。白炽灯稳定运行时，流过的电流是正弦波。但是，白炽灯关闭时，流过的电流是零。也就是说白炽灯打开或关闭的瞬间，电流发生了变化，产生了变化，就产生了谐波！

02谐波电压产生原因

　　那么，谐波电压是如何产生的呢？

　　还以白炽灯为例，小明在白炽灯下读书写字时，小明的白炽灯流过正弦波电流，不产生谐波。但是，同一时间，有千千万万的白炽灯在开启或关闭，这些白炽灯产生了谐波电流。如果这些白炽灯和小明的白炽灯连接在同一个电网。由于供电线路有阻抗，这些白炽灯产生的谐波电流流经供电线路时，会产生谐波电压降，谐波电压降叠加在原先的正弦波电压上，使电网的电压产生谐波，现在，给小明的白炽灯供电的电网也有谐波了！这就是电网谐波电压产生的原因！

　　谐波电流是因、谐波电压是果，谐波电压通过污染电网，对电网上的设备产生各种影响和危害！

　　当然，白炽灯开启或关闭对电网的谐波影响是比较小的。但是，某些大功率冲击负荷，如电弧炼钢炉、轧钢机等，一般出现最大负荷的时间很短，但其峰值可能是其平均负荷的数倍或数十倍。冲击负荷冲击瞬间，会产生较大的谐波，而大量冲击负荷的运行，会产生持续的谐波。

　　就持续影响而言，大功率非线性设备是主要的谐波源。变频器、整流电源等运行时产生较大的谐波电流，谐波电流与整流脉冲数有关。N脉冲整流会产生Nk+1次的谐波，就是说：6脉冲整流会产生6k±1次的谐波，谐波序列为5、7、11、13……，12脉冲整流会产生12k±1次的谐波，谐波序列为11、13、23、25……

　　如果假设交流侧电抗为零，直流电感无穷大的理想情况，这时M次谐波电流的理论相对值为1/M，就是说11次谐波的理论值是1/11，约9%。

　　如果没有安装输入电抗器，12脉整流的主要谐波为11、13、17、19次，总谐波含量约15%。

　　6脉整流输入电流包含6N±1次谐波，主要为5、7、11、13次，5次谐波约20%，7次约14%、11次约9%，13次约8%。总谐波含量约30%。

　　大功率的或数量繁多的非线性设备和冲击负荷，是主要的谐波源。

三谐波分类

　　谐波频率是基波频率的整倍数，法国数学家傅立叶证明，任何重复的波形都可以分解为含有基波频率和一系列为基波倍数的谐波的正弦波分量。

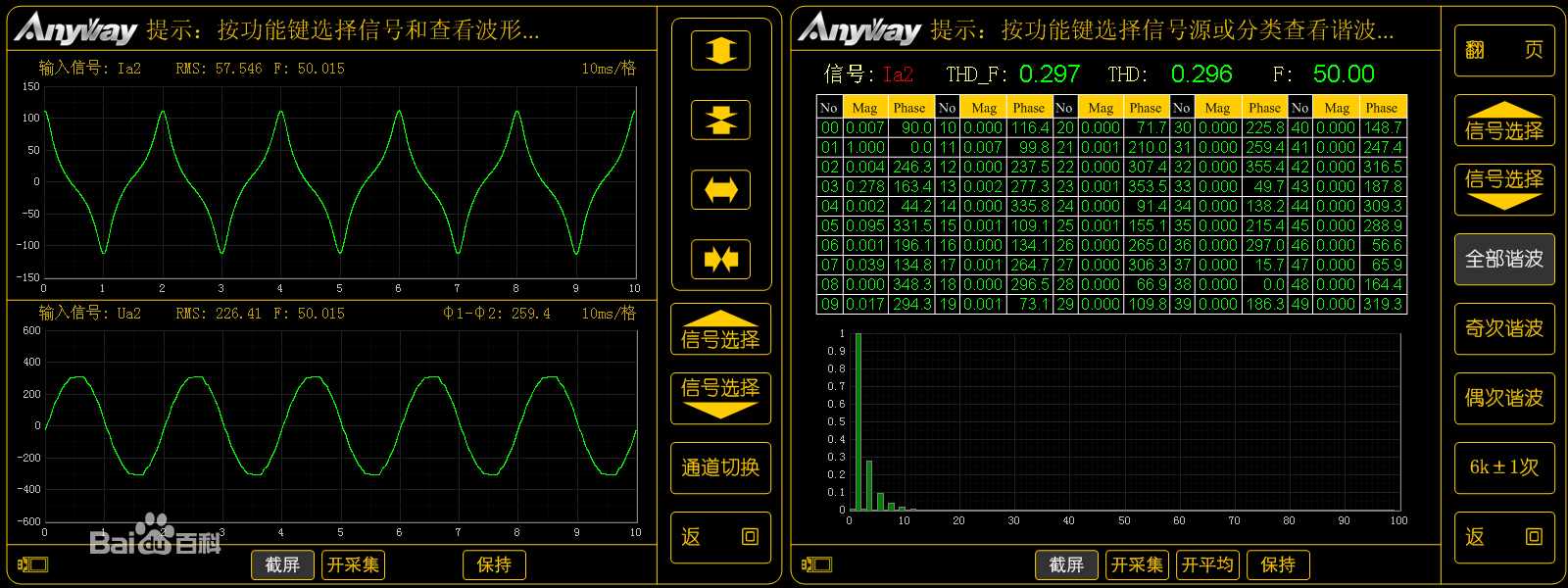
波形及谐波含量

　　根据谐波频率的不同，可以分为：

01偶次谐波

　　额定频率为基波频率偶数倍的谐波，被称为“偶次谐波”，如2、4、6、8次谐波。

02奇次谐波

　　额定频率为基波频率奇数倍的谐波，被称为“奇次谐波”，如3、5、7次谐波

　　一般地讲，奇次谐波引起的危害比偶次谐波更多更大。

　　在平衡的三相系统中，由于对称关系，偶次谐波已经被消除了，奇次谐波占主导地位。对于三相整流负载，出现的谐波电流是6n±1次谐波，例如5、7、11、13、17、19等。六脉整流的三相变频器主要产生5、7次谐波。

03分数次谐波

　　当正弦波分量的频率是原交流信号的频率的非整数倍时，称为分数次谐波，当分数大于1时称为间谐波，当分数小于1时，也称次谐波。

　　严格讲，基于傅里叶变换的谐波分析方法中，不存在分数次谐波。关于分数次谐波与傅里叶变换的关系，请参考”光伏发电站谐波及间谐波相关概念详解“。