正弦电流电路中的有功功率、无功功率、和视在功率三者之间是一个直角三角形的关系，可以通过“复功率”来表示。若用视在功率S表示复功率，则有功功率P为复功率的实部，而无功功率Q为复功率的虚部。在非正弦电路中，无功功率的定义发生了改变，为了与正弦电路的定义相统一，补充了位移无功功率和畸变无功功率的概念，两者的方和根称为广义无功功率。

一无功功率的定义

　　在具有电感和电容等储能元件的电路中，储能元件在半周期的时间里把电源能量变成磁场（或电场）的能量储存起来，在另半周期的时间里对已存的磁场（或电场）能量返回给电源，由于这部分能量只是在储能元件与电源之间进行能量交换，并没有真正被消耗，我们把单位时间内交换能量的振幅值称为无功功率。

　　无功功率用符号Q表示。

　　在《GB/T 2900.1-2008 电工术语 基本术语》中，对无功功率（reactive power）定义如下：

　　对于正弦状态下线性二端元件或二端电路，其量值等于视在功率S和（端子间电压对电流的）相位移角φ的正弦之乘积的量。

二无功功率的单位

　　在国际单位制（SI）中，无功功率的单位为伏安（VA）。在IEC60027-1中给出了无功功率的专用单位名称“乏”和符号Var。

　　无功功率的常用单位还有毫乏（mvar）、千乏（kvar）、兆乏（Mvar）等。

三正弦稳态电路中的无功功率

　　假设交流电周期为T，电压、电流的瞬时值表达式分别为u(t)、i(t)，正弦电路中，电压、电流及瞬时功率的表达式为：

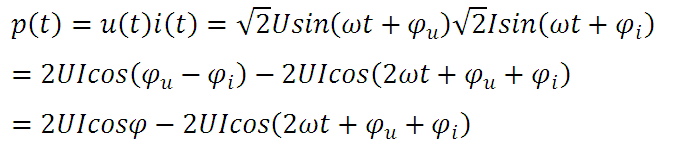
正弦稳态电路的瞬时功率表达式

　　式中：U、I为电压、电流的有效值，ω为角速度，φu为电压的初始相位，φu为电流的初始相位，φ为电压与电流的相位差，即：电流滞后于电压的相位移。

　　因此，正弦稳态电路中，如下图，只要φ≠0°，瞬时功率就会出现负数，表明该电路既会消耗功率，也能发出功率。

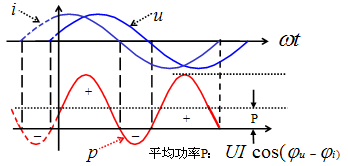
正弦稳态电路中的瞬时功率波形图

　　式中前半部分为常数；后半部分在-2UI和2UI之间变化，且在一个周期内的平均值为零。

　　瞬时功率p(t)在一个周期内的平均值为2UIcosφ。我们称P=2UIcosφ为有功功率。

　　正弦稳态中，储能元件电感或电容的平均功率等于零，不消耗能量，但和电源之间存在能量的交换作用，即在前半个周期吸收电源的功率并储存起来，后半个周期又将其全部释放，这种能量交换的幅度用另外一种功率——无功功率来描述。

　　若将电压相量与电流相量的共轭复数的乘积用复功率表示，其表达式为：

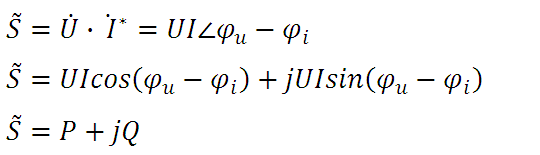
有功功率、无功功率、视在功率及复功率

　　复功率的实部为有功功率，虚部为无功功率，复功率的模为视在功率，这样，有功功率、无功功率、和视在功率三者之间是一个直角三角形的关系。

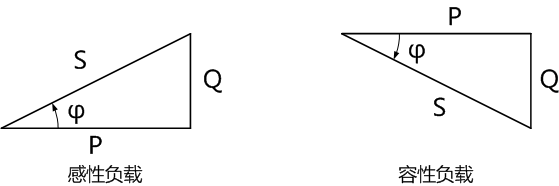
有功功率和无功功率及视在功率构成的复功率三角形

四非正弦电路中的无功功率

　　在非正弦电路中，有功功率和视在功率的定义不变，然而，此时，电压、电流相位差已经没有明确的物理意义，此时，Q按照下述公式定义：

　　

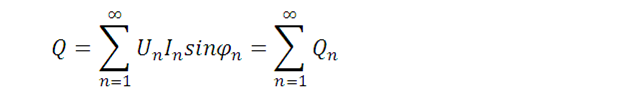
　　式中，U_n、I_n为n次谐波的有效值，当n=1时，U₁、I₁称为基波有效值。

　　然而，此时，

　　

　　为此，引入畸变无功功率D，使下式成立：

　　

　　Q是相同频率的电压分量与电流分量相位移不同产生的无功，称为位移无功功率。而畸变无功功率则是不同频率电压及电流分量之间产生的无功，畸变无功功率计算式如下：

　　

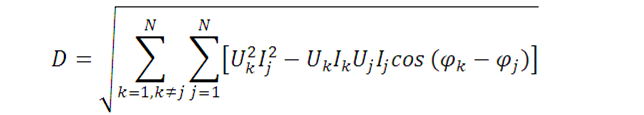
　　某些文献中也将Q称为无功功率，而将Q和D的方和根称为广义无功功率。

五无功功率的正负

　　如下图所示，依据电压与电流的相位差，在0~360°四个象限内，无功功率和无功功率的正负号不同，含义也不同。

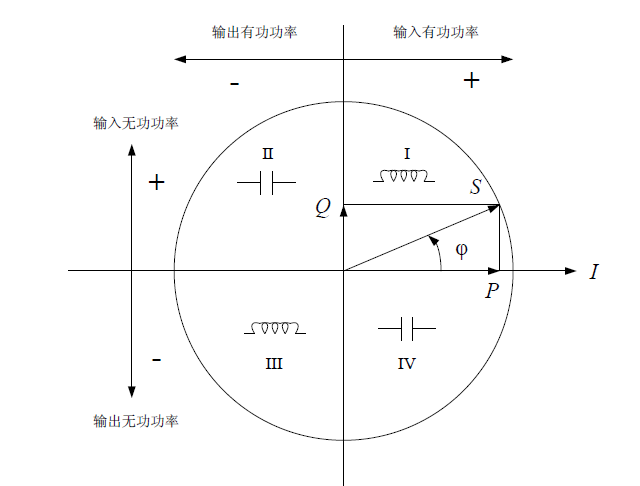
四象限无功功率示意图

　　第一象限为感性负载，输入无功功率为正，输入有功功率为正，可用L+表示；

　　第二象限为容性电源，输入无功功率为正，输入有功功率为负，可用C+表示；

　　第三象限为感性电源，输入无功功率为负，输入有功功率为负，可用L-表示；

　　第四象限为容性负载，输入无功功率为负，输入有功功率为正，可用C-表示。

六无功功率的测量

　　按照变频电量的定义，非正弦电量属于变频电量，全面、准确的测量变频电量的各种特征值，应采用变频功率传感器（或独立的电压、电流传感器）及变频功率分析仪。

　　由于无功功率的定义存在一定的分歧，AnyWay的WP4000变频功率分析仪等仪器在测量非正弦电量时，仪表本身只显示有功功率，无功功率可则通过上位机扩展软件计算显示，用户可根据不同的定义式选择需要的无功功率。

可测量位移无功功率、畸变无功功率的WP4000变频功率分析仪

扩展阅读：

　　银河百科：有功功率

　　　　　　　位移无功功率

　　　　　　　畸变无功功率

　　　　　　　广义无功功率

---